R
rrrFer
Цель работы: приобретение навыков разработки параллельных программ с использованием OpenMP.
Задание
Разработать последовательную и параллельную программы решения СЛАУ матричным методом. Сравнить время работы последовательной и параллельной программ.
Ход работы
Решение системы линейных алгебраических уравнений матричным методом определяется по формуле:

где
 – обратная матрица коэффициентов переменных,
– обратная матрица коэффициентов переменных,
 – матрица-столбец свободных членов,
– матрица-столбец свободных членов,
 – матрица-столбец неизвестных переменных.
– матрица-столбец неизвестных переменных.
Основной задачей в данном методе является вычисление обратной матрицы, зная её, вычислить неизвестные переменные не займет много времени.
В данной работе для поиска обратной матрицы использовались элементарные преобразования матрицы, которые применяются в методе Гаусса решения СЛАУ, таким образом, матрица вида (A|E) приводится к матрице вида (E|
 ), где E – единичная матрица. То есть все те преобразования, которые совершаются над матрицей A, совершаются и над матрицей E. Таким образом, матрица A превратится в единичную, а единичная превратится в матрицу обратную A.
), где E – единичная матрица. То есть все те преобразования, которые совершаются над матрицей A, совершаются и над матрицей E. Таким образом, матрица A превратится в единичную, а единичная превратится в матрицу обратную A.
Описание метода на примерах:
Пример 1. Решить СЛАУ из 3х уравнений:
 ;
;
1 шаг. Составляется матрица коэффициентов неизвестных переменных (A), матрица-столбец свободных членов (B) и единичная матрица (E):
 ;
;
Теперь необходимо привести матрицу A к верхнетреугольному виду, где элементы на главной диагонали равны 1, а элементы ниже главной диагонали равны 0.
2 шаг.
Для начала, если элемент на главной диагонали равен нулю, то необходимо найти строку, где элемент этого же столбца не был равен нулю и поменять местами строки. Если такую строку найти не удалось, то обратная матрица не может быть найдена, как и решение СЛАУ. В данном примере в 1 строке на главной диагонали стоит число 1, значит менять её местами с какой-либо другой строкой не нужно.
3 шаг.
Теперь необходимо разделить каждый элемент текущей строки на элемент, находящийся на главной диагонали, чтобы элемент на главной диагонали стал равен единице. Так как в данном примере элемент уже равен 1, то исходный вид матриц A и E не изменится.
4 шаг.
Далее элементы, находящиеся в столбце под элементом главной диагонали необходимо занулить. Так как на 3м шаге мы превратили элемент на главной диагонали в 1, то из каждой следующей строки можно отнять предыдущую строку, умноженную на элемент 1-го столбца этой строки, таким образом, элемент находящийся в столбце под элементом главной диагонали занулится (например, 7 * 1 – 7 = 0). В данном примере:
После зануления элемента 2й строки:

 ;
;
После зануления элемента 3й строки:

 ;
;
Далее повторяются шаги 2-4 для следующих строк, пока матрица A не примет верхнетреугольный вид.
Для строки 2:
Делим элементы 2 строки на элемент, находящийся на главной диагонали (на 6):
 ;
;
Отнимаем от 3-й строки 2ю, умноженную на единицу:
 ;
;
Делим элементы 3й строки на -2,33:
 ;
;
5 шаг.
Далее происходит обратный ход. Необходимо занулить элементы, находящиеся выше главной диагонали. Алгоритм зануления тот же, что и в прямом ходе, только обход матрицы происходит снизу вверх.
Зануление элемента 2-й строки столбца:
 ;
;
Зануление элемента 3-й строки столбца:
 ;
;
Так как элемент 1 строки, находящийся над элементом главной диагонали во 2м столбце уже равен нулю, то занулять его не нужно.
Таким образом, мы превратили матрицу A в единичную, а единичную в обратную матрицу A, отсюда:
 .
.
Осталось только найти решение СЛАУ умножив обратную матрицу на столбце свободных членов:
 .
.
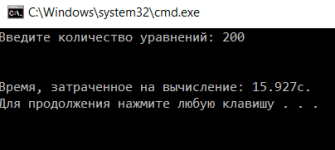
Программы тестировались на СЛАУ из 200 уравнений. Для начала было вычислено среднее время выполнения последовательной программы (рис.1):

Рисунок 1 – результат выполнения последовательной программы
Среднее время выполнения последовательной программы равно 16,2с.
Далее было принято решение распараллелить зануление элементов, лежащих ниже главной диагонали в процессе прямого хода (листинг 1.1) и зануление элементов, лежащих выше главной диагонали в процессе обратного хода (листинг 1.2).
Листинг 1.1. Распараллеленный цикл зануления элементов в процессе прямого хода:
Листинг 1.2. Распараллеленный цикл зануления элементов в процессе обратного хода:
Среднее время выполнения при этом уменьшилось на 12,1 с. и стало равно 4,1 с.
Далее распараллеливается цикл вычисления неизвестных переменных X (листинг 1.3):
Листинг 1.3. Распараллеленный цикл вычисления неизвестных переменных
Среднее время выполнения программы уменьшилось на 0,15 с. и стало равно 3,95 с.
Далее распараллеливается цикл деления каждого элемента строки на элемент этой же строки, лежащий на главной диагонали матрицы (листинг 1.4):
Листинг 1.4. Распараллеленный цикл деления элементов
Среднее время выполнения программы уменьшилось на 0,05 с. и стало равно 3,9 с (рис.2).

Рисунок 2 – результат выполнения параллельной программы
В данной работе коэффициенты переменных и свободные члены генерируются автоматически. Эти числа могут принимать значения от 0 до 100.
Как видно из рисунков 1-4 и таблицы 1, время выполнения параллельной программы меньше времени выполнения последовательной программы в 4 раза. В процессе выполнения параллельной программы все ядра процессора загружены на 100%.
Исходный код параллельной программы представлен в листинге 2. Параллельная программа отличается от последовательной только наличием директив #pragma omp parallel и #pragma omp for. Распараллеливание других циклов или создание параллельных областей либо невозможно, либо не приведет к уменьшению времени выполнения программы
Листинг 2: исходный код параллельной программы:
Вывод:
В данной лабораторной работе были приобретены навыки разработки параллельных программ с использованием OpenMP. Использование параллельных программ позволяет рационально распределить нагрузку на процессор, что значительно сокращает время выполнения программ. В данной работе время решения одной и той же СЛАУ матричным методом различается в 4 раза.
Задание
Разработать последовательную и параллельную программы решения СЛАУ матричным методом. Сравнить время работы последовательной и параллельной программ.
Ход работы
Решение системы линейных алгебраических уравнений матричным методом определяется по формуле:
где
Основной задачей в данном методе является вычисление обратной матрицы, зная её, вычислить неизвестные переменные не займет много времени.
В данной работе для поиска обратной матрицы использовались элементарные преобразования матрицы, которые применяются в методе Гаусса решения СЛАУ, таким образом, матрица вида (A|E) приводится к матрице вида (E|
Описание метода на примерах:
Пример 1. Решить СЛАУ из 3х уравнений:
1 шаг. Составляется матрица коэффициентов неизвестных переменных (A), матрица-столбец свободных членов (B) и единичная матрица (E):
Теперь необходимо привести матрицу A к верхнетреугольному виду, где элементы на главной диагонали равны 1, а элементы ниже главной диагонали равны 0.
2 шаг.
Для начала, если элемент на главной диагонали равен нулю, то необходимо найти строку, где элемент этого же столбца не был равен нулю и поменять местами строки. Если такую строку найти не удалось, то обратная матрица не может быть найдена, как и решение СЛАУ. В данном примере в 1 строке на главной диагонали стоит число 1, значит менять её местами с какой-либо другой строкой не нужно.
3 шаг.
Теперь необходимо разделить каждый элемент текущей строки на элемент, находящийся на главной диагонали, чтобы элемент на главной диагонали стал равен единице. Так как в данном примере элемент уже равен 1, то исходный вид матриц A и E не изменится.
4 шаг.
Далее элементы, находящиеся в столбце под элементом главной диагонали необходимо занулить. Так как на 3м шаге мы превратили элемент на главной диагонали в 1, то из каждой следующей строки можно отнять предыдущую строку, умноженную на элемент 1-го столбца этой строки, таким образом, элемент находящийся в столбце под элементом главной диагонали занулится (например, 7 * 1 – 7 = 0). В данном примере:
После зануления элемента 2й строки:
После зануления элемента 3й строки:
Далее повторяются шаги 2-4 для следующих строк, пока матрица A не примет верхнетреугольный вид.
Для строки 2:
Делим элементы 2 строки на элемент, находящийся на главной диагонали (на 6):
Отнимаем от 3-й строки 2ю, умноженную на единицу:
Делим элементы 3й строки на -2,33:
5 шаг.
Далее происходит обратный ход. Необходимо занулить элементы, находящиеся выше главной диагонали. Алгоритм зануления тот же, что и в прямом ходе, только обход матрицы происходит снизу вверх.
Зануление элемента 2-й строки столбца:
Зануление элемента 3-й строки столбца:
Так как элемент 1 строки, находящийся над элементом главной диагонали во 2м столбце уже равен нулю, то занулять его не нужно.
Таким образом, мы превратили матрицу A в единичную, а единичную в обратную матрицу A, отсюда:
Осталось только найти решение СЛАУ умножив обратную матрицу на столбце свободных членов:
Программы тестировались на СЛАУ из 200 уравнений. Для начала было вычислено среднее время выполнения последовательной программы (рис.1):
Рисунок 1 – результат выполнения последовательной программы
Среднее время выполнения последовательной программы равно 16,2с.
Далее было принято решение распараллелить зануление элементов, лежащих ниже главной диагонали в процессе прямого хода (листинг 1.1) и зануление элементов, лежащих выше главной диагонали в процессе обратного хода (листинг 1.2).
Листинг 1.1. Распараллеленный цикл зануления элементов в процессе прямого хода:
Код:
#pragma omp parallel
{
#pragma omp for
for (int i = k + 1; i < size; i++)
{
double multi = matrix[i][k];
for (int j = 0; j < size; j++)
{
matrix[i][j] -= multi * matrix[k][j];
E[i][j] -= multi * E[k][j];
}
}
}Листинг 1.2. Распараллеленный цикл зануления элементов в процессе обратного хода:
Код:
#pragma omp parallel
{
#pragma omp for
for (int i = k - 1; i > -1; i--)
{
double multi = matrix[i][k];
for (int j = 0; j < size; j++)
{
matrix[i][j] -= multi * matrix[k][j];
E[i][j] -= multi * E[k][j];
}
}
}Среднее время выполнения при этом уменьшилось на 12,1 с. и стало равно 4,1 с.
Далее распараллеливается цикл вычисления неизвестных переменных X (листинг 1.3):
Листинг 1.3. Распараллеленный цикл вычисления неизвестных переменных
Код:
#pragma omp parallel
{
#pragma omp for
for (int i = 0; i < equations_amount; i++)
{
X[i] = 0;
for (int j = 0; j < equations_amount; j++)
X[i] += matrix[i][j] * B[j];
}
}Среднее время выполнения программы уменьшилось на 0,15 с. и стало равно 3,95 с.
Далее распараллеливается цикл деления каждого элемента строки на элемент этой же строки, лежащий на главной диагонали матрицы (листинг 1.4):
Листинг 1.4. Распараллеленный цикл деления элементов
Код:
double div = matrix[k][k];
#pragma omp parallel
{
#pragma omp for
for (int j = 0; j < size; j++)
{
matrix[k][j] /= div;
E[k][j] /= div;
}
}Среднее время выполнения программы уменьшилось на 0,05 с. и стало равно 3,9 с (рис.2).
Рисунок 2 – результат выполнения параллельной программы
В данной работе коэффициенты переменных и свободные члены генерируются автоматически. Эти числа могут принимать значения от 0 до 100.
Как видно из рисунков 1-4 и таблицы 1, время выполнения параллельной программы меньше времени выполнения последовательной программы в 4 раза. В процессе выполнения параллельной программы все ядра процессора загружены на 100%.
Исходный код параллельной программы представлен в листинге 2. Параллельная программа отличается от последовательной только наличием директив #pragma omp parallel и #pragma omp for. Распараллеливание других циклов или создание параллельных областей либо невозможно, либо не приведет к уменьшению времени выполнения программы
Листинг 2: исходный код параллельной программы:
Код:
#include <iostream>
#include <time.h>
#include <omp.h>
#include <vector>
using namespace std;
bool search_reverse_matrix(vector <vector<double>> &matrix)
{
int size = matrix.size();
vector <vector<double>> E(size, vector<double>(size));
//Заполнение единичной матрицы
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
if (i == j) E[i][j] = 1.0;
else E[i][j] = 0.0;
}
}
//Трансформация исходной матрицы в верхнетреугольную
for (int k = 0; k < size; k++)
{
if (abs(matrix[k][k]) < 1e-8)
{
bool changed = false;
for (int i = k + 1; i < size; i++)
{
if (abs(matrix[i][k]) > 1e-8)
{
swap(matrix[k], matrix[i]);
swap(E[k], E[i]);
changed = true;
break;
}
}
if (!changed)
return false;
}
double div = matrix[k][k];
#pragma omp parallel
{
#pragma omp for
for (int j = 0; j < size; j++)
{
matrix[k][j] /= div;
E[k][j] /= div;
}
}
#pragma omp parallel
{
#pragma omp for
for (int i = k + 1; i < size; i++)
{
double multi = matrix[i][k];
for (int j = 0; j < size; j++)
{
matrix[i][j] -= multi * matrix[k][j];
E[i][j] -= multi * E[k][j];
}
}
}
}
//Формирование единичной матрицы из исходной
//и обратной из единичной
for (int k = size - 1; k > 0; k--)
{
#pragma omp parallel
{
#pragma omp for
for (int i = k - 1; i > -1; i--)
{
double multi = matrix[i][k];
for (int j = 0; j < size; j++)
{
matrix[i][j] -= multi * matrix[k][j];
E[i][j] -= multi * E[k][j];
}
}
}
}
matrix = E;
return true;
}
double random(const int min, const int max)
{
if (min == max)
return min;
return min + rand() % (max - min);
}
int main()
{
setlocale(LC_ALL, "RUS");
int equations_amount;
cout << "Введите количество уравнений: ";
cin >> equations_amount;
vector<vector<double>> matrix(equations_amount, vector<double>(equations_amount));
vector<double> B(equations_amount);
// Заполняем матрицу коэффициентов и B
for (int i = 0; i < equations_amount; i++)
{
for (int j = 0; j < equations_amount; j++)
matrix[i][j] = random(0, 100);
B[i] = random(0, 100);
}
// Вывод системы уравнений
/*cout << "\nСистема уравнений:\n";
for (int i = 0; i < equations_amount; i++)
{
for (int j = 0; j < equations_amount; j++)
{
if (j != 0 && matrix[i][j] >= 0)
cout << " +";
cout << " " << matrix[i][j] << "x" << j + 1;
}
cout << " = " << B[i] << endl;
}*/
double t = clock();
// Вычисление обратной матрицы
if (!search_reverse_matrix(matrix))
{
cout << "\nНевозможно найти обратную матрицу!\n";
exit(1);
}
// Матрица-столбец неизвестных X и вычисление окончательного результата
vector<double> X(equations_amount);
#pragma omp parallel
{
#pragma omp for
for (int i = 0; i < equations_amount; i++)
{
X[i] = 0;
for (int j = 0; j < equations_amount; j++)
X[i] += matrix[i][j] * B[j];
}
}
// Вывод окончательного результата
/*cout << "\nРешение системы уравнений:";
for (int i = 0; i < equations_amount; i++)
cout << "\nx" << i + 1 << " = " << X[i];*/
t = (clock() - t) / 1000;
cout << "\n\nВремя, затраченное на вычисление: " << t << "с.\n";
return 0;
}Вывод:
В данной лабораторной работе были приобретены навыки разработки параллельных программ с использованием OpenMP. Использование параллельных программ позволяет рационально распределить нагрузку на процессор, что значительно сокращает время выполнения программ. В данной работе время решения одной и той же СЛАУ матричным методом различается в 4 раза.
Вложения
-
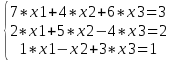 upload_2016-10-4_13-34-0.png1 КБ · Просмотры: 370
upload_2016-10-4_13-34-0.png1 КБ · Просмотры: 370 -
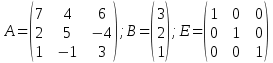 upload_2016-10-4_13-34-0.png1,6 КБ · Просмотры: 277
upload_2016-10-4_13-34-0.png1,6 КБ · Просмотры: 277 -
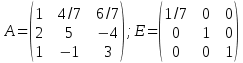 upload_2016-10-4_13-34-0.png1,3 КБ · Просмотры: 330
upload_2016-10-4_13-34-0.png1,3 КБ · Просмотры: 330 -
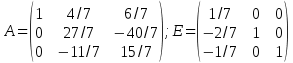 upload_2016-10-4_13-34-0.png1,6 КБ · Просмотры: 261
upload_2016-10-4_13-34-0.png1,6 КБ · Просмотры: 261 -
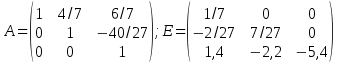 upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 281
upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 281 -
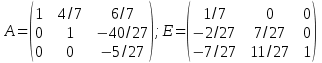 upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 333
upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 333 -
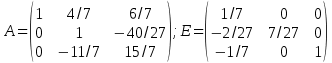 upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 245
upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 245 -
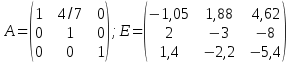 upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 272
upload_2016-10-4_13-34-0.png1,7 КБ · Просмотры: 272 -
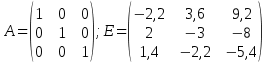 upload_2016-10-4_13-34-0.png1,5 КБ · Просмотры: 290
upload_2016-10-4_13-34-0.png1,5 КБ · Просмотры: 290 -
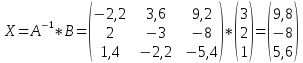 upload_2016-10-4_13-34-0.png1,9 КБ · Просмотры: 313
upload_2016-10-4_13-34-0.png1,9 КБ · Просмотры: 313 -
 upload_2016-10-4_13-37-24.png3,4 КБ · Просмотры: 406
upload_2016-10-4_13-37-24.png3,4 КБ · Просмотры: 406



