Помогите Разобраться С Изменением Сегмента Эллипса В 2d

[oleg-mikhaylov]

Заранее прошу прощения, если не там создал тему.

Ведем разработку векторного редактора. Задача – создать интерфейс управления нарисованным сегментом эллипса (с начальной отрисовкой сегмента проблем нет). Проблема с непониманием математических операций при изменении сегмента.

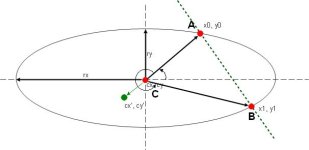
Обратимся к рисунку.
Что мы знаем изначально:
1) начальную и конечную точки дуги и их координаты A(x0, y0) и B(x1, y1)
2) центр образующего дугу эллипса C(cx, cy)
3) полуоси эллипса – rx и ry;
4) любые углы между векторами CA и CB, а также между CA(CB) и полуосями вычисляются.

Предположим мы меняем центр образующего эллипса, перемещаем его в точку с координатами cx', cy'.
Как вычислить новые полуоси эллипса при условии, что точки A и B остаются неподвижными и должны лежать на периметре "нового" эллипса??

 

[oleg-mikhaylov]

Ну пока нет ответов от Математиков докладываю

Я частично разобрался. Всё оказалось очень просто. Я видимо изначально полез в дебри, а решение было на поверхности. Просто надо было вернуться к "истокам".
Каноническое уравнение эллипса:
x^2/rx^2 + y^2/ry^2 = 1

В моем случае есть 2 известные точки на эллипсе с координатами (x0, y0) и (x1, y1) и "новый" центр эллипса (cx', cy')
в результате получаем систему из 2-х уравнений

(cx'-x0)^2/rx^2 + (cy'-y0)^2/ry^2 = 1
(cx'-x1)^2/rx^2 + (cy'-y1)^2/ry^2 = 1

решаем и вот нам счастье - полуоси нашлись и самое интересное - правильно

Теперь новая проблемка в какихто случаях (пока не понял закономернось) одна из полуосей становится равной 0, хотя этого быть не должно (исходя из текушего положения центра и опорных точек) ... может на этот счет будут какие нибудь идеи?

PS: Поправочка. Одна из полуосей НЕ становится равной 0, а происходит деление на 0

 

[Dock1100]

Без самого кода сказать сложно, но поидее это происходит когда кординаты центра по х или у совпадают с соответствующими координатими точек А и Б.

 

[oleg-mikhaylov]

Dock1100

Спасибо, так и было
При решении уравнения в знаменателе появлялась разность квадратов координат центра и одной из точек.
В случае когда они были равны и происходило деление на 0.

А вообще это решение оказалось неудачным. Кроме "неприятностей" с делением на 0 оно еще и не решало поставленной задачи. Точнее решало, но в ОЧЕНЬ частном случае.

Я решил проблему с помощью Аффинных преобразований. Получилось изящно, быстро и без сложной математики.