В этой статейке хочу рассказать про алгоритмы поиска и про то что с ними связано.
Существуют такие алгоритмы:

Каждый алгоритм буду описывать в порядке :идея алгоритма, сложность алгоритма, недостатки алгоритма.
Вы там маякните если что в коментах, могу описать реализацию графов,жадных алгоритмов)
Существуют такие алгоритмы:
- Линейный поиск
- Двоичный поиск
- Бинарное/Двоичное дерево поиска
- Поиск с графами( в глубину,ширину,алгоритм дейкстры)
- Поиск в ХэшТаблице

Каждый алгоритм буду описывать в порядке :идея алгоритма, сложность алгоритма, недостатки алгоритма.
Идея:Последовательный просмотр каждого элемента последовательности, пока не найден нужный
Сложность:Выполняется за один проход цикла, сложность, соответственно – O .
.
Недостатки:Повезет если искомый элемент будет первый в списке, а если он окажется последним? то придется ждать пока алгоритм обползет весь массив, а если в массиве 1ккк элементов?...
Сложность:Выполняется за один проход цикла, сложность, соответственно – O
Недостатки:Повезет если искомый элемент будет первый в списке, а если он окажется последним? то придется ждать пока алгоритм обползет весь массив, а если в массиве 1ккк элементов?...
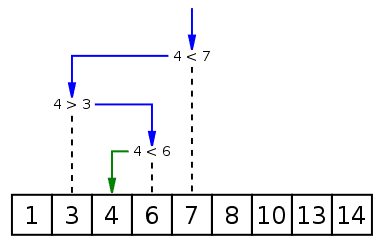
Идея:Поиск по отсортированному массиву.Осуществляется за счет дробления массива пополам. Берется центральный элемент массива,проверяется равен ли он искомому,да-профит,нет-сверяем меньше или больше центрального элемента мы ищем. Если больше переходим в правую часть ( массив [x..n]), если меньше то соответственно в левую часть( массив [i..x]). Далее повторяем процедуру рекурсивно.

Сложность:Сложность – O(log ).
).
Недостатки:Не каждый массив будет отсортирован.
Пример кода на питоне:
Сложность:Сложность – O(log
Недостатки:Не каждый массив будет отсортирован.
Пример кода на питоне:
Код:
def bin_search(lst, x):
lower_bound = 0
upper_bound = len(lst)
while lower_bound != upper_bound:
compared_value = (lower_bound + upper_bound) // 2 # Целочисленный тип в Python имеет неограниченную длину
if x == lst[compared_value]:
return x
elif x < lst[compared_value]:
upper_bound = compared_value
else:
lower_bound = compared_value + 1
return None # если цикл окончен, то значение не найденноИдея: Хэш функция представляет собой функцию, которая принимает строку а возвращает число.Связываем воедино хэшфункцию и массив и получается хэштаблица. В любом приличном языке существует реализация хештаблиц.В Python тоже есть хеш-таблицы они называются словарями.

Выполняет поиск мгновенно, независимо от числа элементов в массиве.Для каждого значения-свой ключ. И программа при вызове поиска определенного значения сразу знает по какому адресу в памяти обратиться.
Сложность:Выполняется за постоянное время, но худшем случае за линейное.
Недостатки: Не могут хранить в себе одинаковые значения, при большом количестве колизий и малом коэффициенте заполнения время работы увеличивается.
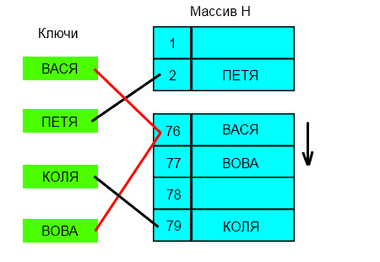
Выполняет поиск мгновенно, независимо от числа элементов в массиве.Для каждого значения-свой ключ. И программа при вызове поиска определенного значения сразу знает по какому адресу в памяти обратиться.
Сложность:Выполняется за постоянное время, но худшем случае за линейное.
Недостатки: Не могут хранить в себе одинаковые значения, при большом количестве колизий и малом коэффициенте заполнения время работы увеличивается.
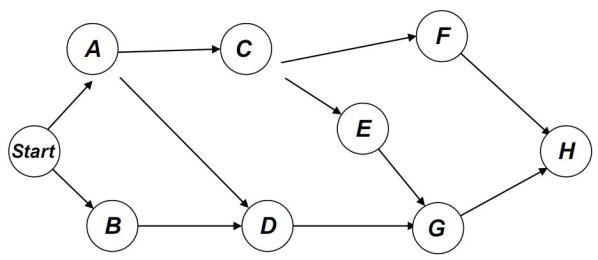
Сложно обьясняемая мной тема, поэтому просто посмотрите

Ссылка скрыта от гостей
Ссылка скрыта от гостей
Ссылка скрыта от гостей
Вы там маякните если что в коментах, могу описать реализацию графов,жадных алгоритмов)




