Генерация больших простых чисел Python

shinenvice034 · 05.10.2020

Требуется помощь в создании алгоритма, которой генерирует простое(!) число длинной от 9 и более цифр.

Topaz33 · 06.10.2020

В каком смысле простое? Вы про что? Можно больше конкретики?

f22 · 06.10.2020

Жуков Сергей сказал(а):
В каком смысле простое? Вы про что? Можно больше конкретики?

Ссылка скрыта от гостей

shinenvice034 сказал(а):
Требуется помощь в создании алгоритма, которой генерирует простое(!) число длинной от 9 и более цифр.

Да вроде бы всё просто:
Исходя из определения, вам нужно просто проверять, делится ли каждое число, меньше заданного, на какие-то меньше себя без остатка.

То есть должно быть 2 цикла, один главный, один вложенный.
В первом перебираются числа от 9 символов -

Python:

for target_num in range(100000000, тут указываете верхнюю границу)

А вложенный цикл будет пробегать от 2 до этого числа и проверять, есть ли остаток от деления
В целом код может выглядеть так

Python:

primes = []
for target_num in range(100000000, 200000000):
  is_prime = True
  for i in range(2, target_num):
    if target_num % i == 0:
      is_prime = False
  if is_prime:
    primes.append(target_num)

print(primes)

Если нужно в бесконечном цикле то как-то так

Python:

primes = []
target_num = 100000000

while True:
  is_prime = True
  for i in range(2, target_num):
    if target_num % i == 0:
      is_prime = False
  if is_prime:
    primes.append(target_num)
  target_num += 1

print(primes)

Есть мнение, что можно пробегаться не по всему списку чисел от 2 до target_num,а до

Python:

for i in range(2, int((target_num ** 0.5)) + 1):

Proxy n1nja · 06.10.2020

Если честно не очень понял твое условие, но если нужное случайное число от N количества знаков, то могу предложить тебе такой вот вариант

Python:

import random


def generate_random_number(number_length: int = 9) -> int:
    result: list = []
    for _ in range(0, number_length):
        result.append(f"{random.randint(0, 9)}")
        if result[0] == '0':
            result[0] = f"{random.randint(0, 9)}"
    return int(''.join(result))


def checking_number_prime(number: int = 10) -> bool:
    divisor = 2
    while number % divisor != 0:
        divisor += 1
    return divisor == number


if __name__ == '__main__':
    while True:
        user_input = input('enter the length of the number: ')
        if user_input.isdigit():
            random_number = generate_random_number(int(user_input))
            if checking_number_prime(number=random_number):
                print(random_number, '- prime number')
            else:
                print(random_number, '- composite number')

Функция generate_random_number принимает на вход аргумент, какой длины должно быть число и возвращает число, заданной длины. Функция checking_number_prime принимает на вход любое число и возвращает ответ, является ли число простым.

П.С.
На правах рекламы. Подписывайся на нашу группу питонистов кодебая, там тебе всегда помогут [GROUP=14]ТЫК[/GROUP]

f22 · 06.10.2020

Proxy n1nja сказал(а):

Python:

def generate_random_number(number_length: int = 9):
    result = ''.join(["%s" % random.randint(0, 9) for _ in range(0, number_length)])
    if result.isdigit():
        return int(result)
    return result

Какой же странный у вас код.
Зачем нужна проверка числа на число? Как можно из n чисел получить не число представить сложно.
Тогда уж просто возвращайте

Python:

def generate_random_number(number_length: int = 9):
    return int(''.join(["%s" % random.randint(0, 9) for _ in range(0, number_length)]))

ну или

Python:

random.randint(int('1' + '0' * (number_length - 1)), int('9' * number_length))

Я бы понял, если бы int имел какие-то ограничения на размер, но их, увы и ах, в Python нет...

Python:

print(type(int(10^1000000)))

Proxy n1nja сказал(а):
run = True

Зачем нужна ещё одна переменная, а не просто

Python:

while True:

И самое главное:

Proxy n1nja сказал(а):
if number % 2 == 0:

почему вы решили, что простое число это - чётное число?

Proxy n1nja · 06.10.2020

f22 сказал(а):
Какой же странный у вас код.

Судя по всему пока ты писал комментарий, большинство косяков я уже и сам увидел и поправил. Это все происходит потому что, я думаю мол надо сделать проверку на ввод, написал кусочек, закинул на форум, потом начал дописывать дальше, мысль про проверку осталась, и закрутил по второму кругу ну и всякое такое, в общем спешка и невнимательность.
По поводу простых\четных, увидел только сейчас добравшись до домашнего компьютера и так же пофиксил.

PyataCHOK · 06.10.2020

Proxy n1nja сказал(а):
По поводу простых\четных, увидел только сейчас добравшись до домашнего компьютера и так же пофиксил.

Зря ты оправдывался, мой АКЕЛЛА. Маугли щас заступится за вожака.
Алгоритм от F22 также плох, как и твой.
У него даже нет никакого алгоритма, он попросту спрятался за красивыми фразами.
Если бы на основе умозаключений f22 кто-то написал алгоритм и запустил его(алгоритм) то стало-бы очевидным никудышность всего того, что представлено выше.

Между тем, решение давно рассмотрено в учебнике кандидата технических наук, доцента Златопольского Дмитрия Михайловича "Основы программирования на язые Python"
Страница 120 -121.

Во времена совка такие задачи каждый олимпиадник щёлкал в считанные минуты, а не глотал ноотропин с глицином.

f22 · 06.10.2020

PyataCHOK сказал(а):
Зря ты оправдывался, мой АКЕЛЛА. Маугли щас заступится за вожака.
Алгоритм от F22 также плох, как и твой.
У него даже нет никакого алгоритма, он попросту спрятался за красивыми фразами.
Если бы на основе умозаключений f22 кто-то написал алгоритм и запустил его(алгоритм) то стало-бы очевидным никудышность всего того, что представлено выше.

Между тем, решение давно рассмотрено в учебнике кандидата технических наук, доцента Златопольского Дмитрия Михайловича "Основы программирования на язые Python"
Страница 120 -121.

Во времена совка такие задачи каждый олимпиадник щёлкал в считанные минуты, а не глотал ноотропин с глицином.

Не поленился и нашёл творчество этого автора. Даже страницу нашёл и код перепечатал...

Могу сказать, что вы не правы.
На бОльших объёмах, код приведённый мной показывает лучшие результаты. Можете проверить сами

Python:

from datetime import datetime

def prime_book(n):
    if n == 2:
        # print('Это число простое')
        return n
    if n % 2 == 0 and n != 2:
        # print('Это число простым не является')
        pass
    if n % 2 == 1:
        kol_del = 2 #Учитываем как делители числа 1 и n
        for vdel in range(3, n//3 + 1, 2): #Рассматриваем нечетные числа
            if n % vdel == 0:
                kol_del = kol_del + 1
        if kol_del == 2:
            # print('Это число простое')
            return n
        # else:
            # print('Это число простым не является')
           
def prime_new(n):
    is_prime = True
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            is_prime = False
            break
    if is_prime:
        return n

for counts in [10, 100, 1000, 10000, 20000, 40000]:
    print("Диапазон поиска чисел: от 1 до", counts)
    results_book = []
    results_new = []

    start_time_first = datetime.now()
    for i in range(1, counts):
        res = prime_book(i)
        if res:
            results_book.append(res)

    print("Время Златопольского:", datetime.now() - start_time_first)
    print("Количество найденных чисел:", len(results_book))
   
    start_time_second = datetime.now()
    for i in range(1, counts):
        res = prime_new(i)
        if res:
            results_new.append(res)

    print("Время нового кода:", datetime.now() - start_time_second)
    print("Количество найденных чисел:", len(results_new))

    print("Списки равны?", results_book == results_new)
    print()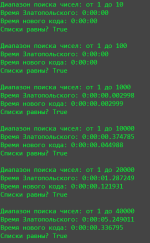

Результаты на двух разных машинах

PyataCHOK сказал(а):
У него даже нет никакого алгоритма, он попросту спрятался за красивыми фразами.
Если бы на основе умозаключений f22 кто-то написал алгоритм и запустил его(алгоритм) то стало-бы очевидным никудышность всего того, что представлено выше.

Смелости признать свою ошибку хватит?

PyataCHOK · 06.10.2020

f22 сказал(а):
Смелости признать свою ошибку хватит?

Хватит. Мог-бы предположить, что я предвидел такую твою реакцию заранее.
У меня в отличие от тебя короны на голове нет.
Приведенный тобою код из книги Златопольского - это попытка пустить пыль окружающим в глаза.
Горе - математик.
Читай страницу 121, где Златопольский предлагает исключить из алгоритма все делители, меньшие чем корень квадратный из возможного делителя.
А ещё далее он предлагает и ещё более радикальное решение.
Математика прошла мимо тебя, f22

Жду извинений.

f22 · 06.10.2020

PyataCHOK сказал(а):
Жду извинений.

И за что вы хотите извинений?
Или снова не на той странице открыл?

Python:

from datetime import datetime

def prime_book(n):
    if n == 2:
        # print('Это число простое')
        return n
    if n % 2 == 1:
        kol_del = 2 #Учитываем как делители числа 1 и n
        for vdel in range(3, n//3 + 1, 2): #Рассматриваем нечетные числа
            if n % vdel == 0:
                kol_del = kol_del + 1
        if kol_del == 2:
            # print('Это число простое')
            return n
        # else:
            # print('Это число простым не является')

def prim_book_122(n):
    if n == 2:
        # print('Это число простое')
        return n
    if n % 2 == 1:
        kol_del = 2 #Учитываем как делители числа 1 и n
        vdel = 3
        while vdel * vdel <= n:
            if n % vdel == 0:
                kol_del = kol_del + 1
                break
            vdel = vdel + 2
        if kol_del == 2:
            # print('Это число простое')
            return n
        # else:
            # print('Это число простым не является')


def prime_new(n):
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            break
    else:
        return n


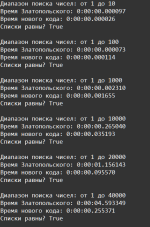
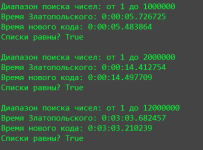
for counts in [50000, 100000, 1000000, 2000000, 10000000]:
    print("Диапазон поиска чисел: от 1 до", counts)
    results_book = []
    results_new = []

    start_time_first = datetime.now()
    for i in range(1, counts):
        res = prim_book_122(i)
        if res:
            results_book.append(res)

    print("Время Златопольского:", datetime.now() - start_time_first)
    # print("Количество найденных чисел:", len(results_book))

    start_time_second = datetime.now()
    for i in range(1, counts):
        res = prime_new(i)
        if res:
            results_new.append(res)

    print("Время нового кода:", datetime.now() - start_time_second)
    # print("Количество найденных чисел:", len(results_new))

    print("Списки равны?", results_book == results_new)
    print()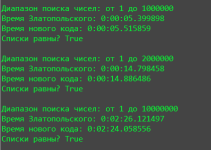

PyataCHOK сказал(а):
У него даже нет никакого алгоритма, он попросту спрятался за красивыми фразами.

PyataCHOK сказал(а):
У меня в отличие от тебя короны на голове нет.

PyataCHOK сказал(а):
Горе - математик.

PyataCHOK сказал(а):
Математика прошла мимо тебя, f22

И оставьте свою поганую манеру переходить на личности.
Будете продолжать, применю санкции.

PyataCHOK · 06.10.2020

Ваши скриншоты не убедительны.
Вы попросту хотите выйти сухим из неприятной ситуации, которую сами создали.
Непонятно, зачем Вам нужны были мои извинения, никто за язык вас не тянул.
Мне Ваши извинения - что зайцу тормоз.

Proxy n1nja · 07.10.2020

f22 сказал(а):
Могу сказать, что вы не правы.
На Больших объёмах, код приведённый мной показывает лучшие результаты. Можете проверить сами

Проверил, могу сказать ты не прав. Пруфы будут ниже.
Короче, раз пошла пляска про алгоритмы, есть такая штука как "Решето Эратосфена", это самый быстрый известный мне алгоритм нахождения простых чисел.

Привожу пример в коде ниже, а так же сравниваем скорость выполнения алгортимов:
(сразу оговорюсь, что код из книги Златопольского я мог понять не верно и хрени понаписать, если что, поправьте его в ответах)

Python:

import time


def get_runtime(func):
    def wrapper(arg):
        print("Диапазон поиска чисел: от 1 до", arg)
        start_time = time.monotonic()
        print(func(arg))
        print('Время выполнения: ', time.monotonic() - start_time)

    return wrapper


@get_runtime
def sieve_eratosthenes(n):
    """
    Решето Эратосфена
    """
    a = range(n + 1)
    a = list(a)
    a[1] = 0
    result_list = []
    i = 2
    while i <= n:
        if a[i] != 0:
            result_list.append(a[i])
            for j in range(i, n + 1, i):
                a[j] = 0
        i += 1
    return result_list


@get_runtime
def zlatapolski_code(a):
    """
    Код из книги Златопольского
    """
    result = []
    for n in range(a):
        if n == 2:
            result.append(n)
        if n % 2 == 1:
            kol_del = 2  # Учитываем как делители числа 1 и n
            for vdel in range(3, n // 3 + 1, 2):  # Рассматриваем нечетные числа
                if n % vdel == 0:
                    kol_del = kol_del + 1
            if kol_del == 2:
                result.append(n)
            else:
                continue
    return result


@get_runtime
def f22(n):
    """
    Код пользователя f22
    """
    primes = []
    for target_num in range(1, n):
        is_prime = True
        for i in range(2, target_num):
            if target_num % i == 0:
                is_prime = False
        if is_prime:
            primes.append(target_num)

    return primes


if __name__ == '__main__':
    test_number = 100000
    print('\n')
    print('Решето Эратосфена')
    sieve_eratosthenes(test_number)
    print('\n')
    print('Код из книги Златопольского')
    zlatapolski_code(test_number)
    print('\n')
    print('Код комрада f22')
    f22(test_number)

А теперь немного о тестах на ведре, с которого мне приходится работать.

Первый тест:

Ну собственно код каждой из функций выполнен мгновенно. Насчет является ли 1 простым числом или нет, сейчас не будем разводить холивар, просто приведу цитату из википедии

В настоящее время в математике принято не относить единицу ни к простым, ни к составным числам, так как это нарушает важную для теории чисел единственность разложения на простые множители. Последним из профессиональных математиков, кто рассматривал 1 как простое число, был Анри Лебег в 1899 году.

Едем дальше и запускаем второй тест:

Код из книги Златопольского как и "решето Эратосфена" отрабатывают мгновенно а вот код товарища @f22 начинает немного сдавать позиции.
Третий тест:

Думаю все наглядно. Если будет желание, выложите ваши результаты.
В теории результаты можно ускорить используя генераторы списков и вместо привычного интерпретатора питона, интерпретатор pypy.

P.S.
Сообщество которое докапывается до сути:
[GROUP=14][/GROUP]

f22 · 07.10.2020

Proxy n1nja сказал(а):
Проверил, могу сказать ты не прав. Пруфы будут ниже.

Немного изменил свой код, исключив чётные числа из проверки, стал ещё сильнее опережать код Златопольского

Python:

@get_runtime
def f22(n):
    """
    Код пользователя f22
    """
    primes = [ ]
    for target_num in range(1, n):
        if target_num != 2 and target_num % 2 == 0:
            continue
        for i in range(2, int(target_num**0.5) + 1):
            if target_num % i == 0:
                break
        else:
            primes.append(target_num)

    return primes

Что скажете?

Proxy n1nja · 07.10.2020

f22 сказал(а):
Немного изменил свой код, исключив чётные числа из проверки, стал ещё сильнее опережать код Златопольского

Python:

@get_runtime def f22(n): """ Код пользователя f22 """ primes = [ ] for target_num in range(1, n): if target_num != 2 and target_num % 2 == 0: continue for i in range(2, int(target_num**0.5) + 1): if target_num % i == 0: break else: primes.append(target_num) return primes

Что скажете?

Проверил и вот результат:

Да, он стал работать быстрее чем код из книги (с тем учетом, что я его правильно понял и так же правильно написал, если что пусть поправят.)
Но опять же, он будет работать медленнее чем решето

Вот на скрине это наглядно видно:

Вывод массивов убрал, потому что столкнулся с багом в пичарме, при котором первые три принта перестает быть видно при выводе таких длинных строк.

f22 · 07.10.2020

Proxy n1nja сказал(а):
Но опять же, он будет работать медленнее чем решето

Куда уж мне с Эратосфеном тягаться ))
Смысл изменений тут довольно простой: делитель простого числа не может быть чётным.
То есть если сам делитель делится на 2 и проверяемое число не равно 2, то это точно не простое число и проверять все числа до него не имеет смысла.

Proxy n1nja сказал(а):
Да, он стал работать быстрее чем код из книги

Именно это я и хотел от вам услышать. Спасибо!

PyataCHOK · 08.10.2020

Вот работа программ на больших числах:

Код f22:

Python:

#! /usr/bin/env python3
# -*- coding: utf-8 -*-
import math
from time import time
# https://codeby.net/threads/generacija-bolshix-prostyx-chisel-python.75268/#post-392311
# от f22


def f22():
    """
    Код пользователя f22
    """
    for target_num in range(1, 110000000):
        if target_num != 2 and target_num % 2 == 0:
            continue
        for i in range(2, int(target_num**0.5) + 1):
            if target_num % i == 0:
                break
        else:
            print(target_num, "- Простое число.")


def main():
    start_time = time()
    f22()
    print("Затраченное время: ", time() - start_time)


if __name__ == "__main__":
    main()


# 109999957 Простое число
# 109999993 Простое число
# Затраченное время:  2738.3991611003876

Замеры времени кода от f22

Python:

#! /usr/bin/env python3
# -*- coding: utf-8 -*-
import math
from time import time
# https://codeby.net/threads/generacija-bolshix-prostyx-chisel-python.75268/#post-392311
# Златопольский стр. 121


def prime_book(n):
#    print("Проверка числа: ", n)
    k = 1                # Переменная - счётчик
    x = 1                # Первый возможный делитель
    while x * x <= n:
#        print("Проверяю делитель :", x)
#        print("Остаток от деления: ",n % x)
        if n % x == 0:
            k += 1       # Увеличиваем счётчик
            if k > 2:
                break    # Если количество делителей более 2, то прекращаем цикл, так как число не простое.
        x = x + 2        # Увеличиваем возможный делитель на 2, тем самым исключая из генератора чётные делители
#    print("Количество делителей: ", k)
    if k == 2:
        print(n, "- простое число.")
#    else:
#        print(n, "- число составное.")



def main():
    start_time = time()
    for n in range(1, 110000000, 2):
        prime_book(n)
    print("Затраченное время: ", time() - start_time)


if __name__ == "__main__":
    main()


# 109999993 - простое число.
# Затраченное время:  2550.288964509964

Замеры времени алгоритма из учебника Златопольского.

f22 сказал(а):
Немного изменил свой код, исключив чётные числа из проверки, стал ещё сильнее опережать код Златопольского

А на мысль об изменении кода вам не Златопольский подсказал ?

После Ваших утренних изменений оба кода - аналогичны.

Все сервисы Codeby

Поиск

Поиск

Генерация больших простых чисел Python

shinenvice034

Active member

Topaz33

Well-known member

f22

Codeby Academy

Proxy n1nja

f22

Codeby Academy

Proxy n1nja

PyataCHOK

f22

Codeby Academy

PyataCHOK

f22

Codeby Academy

PyataCHOK

Proxy n1nja

f22

Codeby Academy

Proxy n1nja

f22

Codeby Academy

PyataCHOK